Fibonacci Heap
The Fibonacci Heap is the famous data structure that allows to decrease the running time of Dijkstra’s algorithm
from \(O((V+E)\log V)\) to \(O(V\log V + E)\) since it implements the decrease_key operation in \(\Theta(1)\) amortized time.
It also support a set of operations that make it a “mergeable heap” (see mergeable heap).
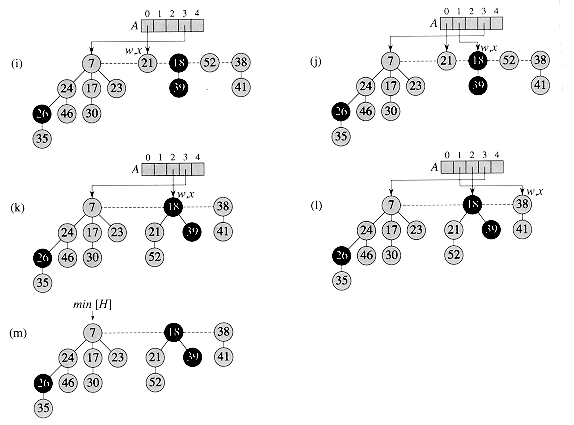
To achieve such performance a fibonacci heap is basically a linked list of min-heap-ordered rooted trees (that are, in turn, implemented as linked list of smaller min-heap-ordered rooted tree). To implement the structure we first need to implement the template for a linked list (since it will be a linked list of fibonacci nodes that are not yet defined we need to use a template).
The linked list need to support just a few basic operations
-
push_backappend a node to the list -
extract_nodeextract a specific node without modifying its pointers -
remove_nodecompletely remove a node by extracting it and clearing its pointers. -
clearclears the list
Such list should look something like this.
#include <iostream>
template <typename T>
class doubly_linked_list {
private:
size_t _size;
public:
T head;
doubly_linked_list() : head(nullptr), _size(0) {};
~doubly_linked_list() {};
void init() {
head = nullptr, _size = 0;
}
void insert_node(T prev, T node) {
if (prev != nullptr) {
node->left = prev;
node->right = prev->right;
prev->right->left = node;
prev->right = node;
}
++_size;
}
void extract_node(T node) {
if (_size == 1) head = nullptr;
else if (node == head) head = node->right;
node->right->left = node->left;
node->left->right = node->right;
--_size;
}
void remove_node(T node) {
extract_node(node);
node->left = node;
node->right = node;
}
void push_back(T node) {
if (empty()) insert_node(head = node, node);
else insert_node(head->left, node);
}
bool empty() {
return _size == 0;
}
int size() {
return _size;
}
void clear(T &x) {
head = nullptr, _size = 0, x = nullptr;
}
};
Now it’s time to implement the fibonacci heap’s node. The nodes are the most important part of the whole structure.
As happens with any other nodes of a heap, a fibonacci heap’s node has key and data attributes and, since it’s a element of a linked list, it also has two pointer left and right that points to its neighbors. Each node could potentially be the root of a sub tree, for that reasons it need to store the number of its child, using the degree attribute. A boolean attribute mark it’s used to keep track if a node has lost a child.
template <typename KEY_NODE, typename DATA_NODE>
class fibonacci_node {
public:
fibonacci_node<KEY_NODE, DATA_NODE> *p, *left, *right;
doubly_linked_list<fibonacci_node<KEY_NODE, DATA_NODE> *> child_list;
int degree;
bool mark;
KEY_NODE key;
DATA_NODE data;
fibonacci_node() : p(nullptr), left(this), right(this), child_list(), degree(0), mark(false) {}
// If obj are modified after being insrted something bad could happen
fibonacci_node(KEY_NODE &k, DATA_NODE &d) : fibonacci_node<KEY_NODE, DATA_NODE>() {
key = k;
data = d;
}
bool operator< (const fibonacci_node x){ return key < x.key; }
bool operator> (const fibonacci_node x){ return key > x.key; }
};
Finally it comes the actual structure. A fibonacci heap has some utility method that are used by the other procedure, those are:
-
consolidaterearrange the internal structure after the minimum element if extracted. -
cutcut the link between a node x and its parent making x a root. -
cascading_cutrecursively cut nodes until it find a root or an unmarked node. -
make_childtakes two nodes and make one child of the other. -
max_degreereturn the maximum number of nodes in the root list.
The public methods implemented below are the following (what they do is self explanatory):
insert-
extract_minboth delete and return the element whose key is minimum -
decrease_minother method that have not been implements but that could be useful are: union and delete.
To make decrease_key work in constant time it’s also necessary to get, in constant time, a node given its key. To do that I used a hash table (implemented with an unordered_map) to map each key to the address of its corresponding node.
#include <cmath>
#include <unordered_map>
template <typename KEY, typename DATA>
class fibonacci_heap {
private:
int nodes;
fibonacci_node<KEY, DATA> *min_node;
doubly_linked_list<fibonacci_node<KEY, DATA> *> root_list;
std::unordered_map<KEY, fibonacci_node<KEY, DATA> *> addresses;
fibonacci_node<KEY, DATA> *child;
fibonacci_node<KEY, DATA> *extracted;
void consolidate() {
std::vector<fibonacci_node<KEY, DATA> *> pointer(max_degree(), nullptr);
fibonacci_node<KEY, DATA> *node = min_node, *x, *y;
for(int i=0; i<root_list.size(); ++i){
node = (x = node)->right;
int d = x->degree;
while (pointer[d]) {
y = pointer[d];
if (*x > *y)
std::swap(x, y);
make_child(y, x);
pointer[d] = nullptr;
++d;
--i;
}
pointer[d] = x;
}
root_list.clear(min_node);
for (auto &x: pointer) {
if (x) {
root_list.push_back(x);
if (min_node == nullptr)
min_node = x;
else if (*x < *min_node)
min_node = x;
}
}
}
void cut(fibonacci_node<KEY, DATA> *x, fibonacci_node<KEY, DATA> *y) {
y->child_list.remove_node(x);
--y->degree;
root_list.push_back(x);
x->p = nullptr;
x->mark = false;
}
void cascading_cut(fibonacci_node<KEY, DATA> *y) {
fibonacci_node<KEY, DATA> *z = y->p;
while(z != nullptr){
if(y->mark == false){
y->mark = true;
z = nullptr;
} else {
cut(y, z);
z = (y = z)->p;
}
}
}
void make_child(fibonacci_node<KEY, DATA> *y, fibonacci_node<KEY, DATA> *x) {
root_list.remove_node(y);
x->child_list.push_back(y);
++x->degree;
y->p = x;
y->mark = false;
}
// upper_bound of number of root nodes in the root lists that will be present after consolidation
int max_degree() { return (int)floor(log((double)nodes)/log((1.0+sqrt(5.0))/2.0))+1; }
public:
fibonacci_heap(int size, int value) : nodes(0), min_node(nullptr), addresses() {
fill(size, value);
}
fibonacci_heap(int size) : nodes(0), min_node(nullptr), addresses(size) {}
~fibonacci_heap() {};
void fill(int size, int value){
for(int i=0; i<size; ++i)
insert(new fibonacci_node<KEY, DATA>(i, value));
}
bool empty() { return !nodes; }
void insert(KEY k, DATA d) {
fibonacci_node<KEY, DATA> *node = new fibonacci_node<KEY, DATA>(k, d);
addresses[node->key] = node;
root_list.push_back(node);
if (min_node == nullptr)
min_node = node;
else if(*node < *min_node)
min_node = node;
++nodes;
}
fibonacci_node<KEY, DATA> extract_min(){
extracted = min_node;
if (extracted != nullptr) {
while (extracted->child_list.size()) {
child = extracted->child_list.head->left;
extracted->child_list.remove_node(child);
child->p = nullptr;
root_list.push_back(child);
}
root_list.extract_node(extracted);
if (extracted == extracted->right) {
min_node = nullptr;
} else {
min_node = extracted->right;
consolidate();
}
--nodes;
addresses.erase(extracted->key);
}
fibonacci_node<KEY, DATA> x(extracted);
return x;
}
void decrease_key(int data, int key) {
fibonacci_node<KEY, DATA> *x = (*addresses)[data];
if (key < x->key) {
x->key = key;
fibonacci_node<KEY, DATA> *y = x->p;
if (y != nullptr && *x < *y) {
cut(x, y);
cascading_cut(y);
}
if (*x < *min_node)
min_node = x;
}
}
};
Although the asymptotic running time for decrease_key is constant the structure itself is quite slow because of the complex internal structure that need to be updated. Such implementation uses template and it has been tested and should be bug free.
Here is the link on GitHub of the complete implementation: fibonacci heap
Enjoy Reading This Article?
Here are some more articles you might like to read next: